Contents

Abstract and Introduction

Page 1

  • Solely based on RL without data, guidance or domain knowledge beyond rules
  • Precise and sophisticated lookahead needed for a game like Go

Page 2

  • AlphaGo Fan, which defeated European champion Fan Hui, had a policy neural network trained to predict expert moves and a value neural net trainer to predict winners of games that policy network played against itself
  • Trained nets combined with MCTS to provide lookahead search using policy net to narrow search to high probability moves and value net along with MC rollouts to evaluate tree positions
  • This was followed by a similar model Alpha Go Lee which defeated Lee Sedol
  • AlphaGo Zero different as follows
    1. Trained solely by self-play RL, starting with random moves
    2. Only black and white stones as input features
    3. Single net not policy and value
    4. Simpler tree search without MC rollouts
  • Achieves via RL algorithm that incorporates lookahead search inside training loop - result is rapid improvement and precise and stable learning

1. Reinforcement Learning in AlphaGo Zero

Page 3 (last paragraph continues into Page 5)

  • Neural net $f_\theta$ takes as input a raw board representation of the position $s$ and its history and outputs $(\mathbf{p}, v)$ where $p_a = \mathrm{Pr}(a\vert s)$.
  • In each position MCTS is executed with the help of the net and outputs new probabilities $\boldsymbol{\pi}$ for playing each move.
  • $\boldsymbol{\pi}$ tends to result in much stronger moves than the raw probabilities $\mathbf{p}$.
  • Can see MCTS as a policy improvement operator.
  • Self-play with search - using $\boldsymbol{\pi}$ to make the move and using winner $z$ as sample of the value can be seen as policy evaluation operator.
  • Main idea of RL algorithm is to use these search operators repeatedly in policy iteration whereby neural net parameters are updated to make $(\mathbf{p}, v)$ closely match $(\boldsymbol{\pi}, z)$.
  • The improved parameters are then used in the next iteration to make the search even stronger.
  • MCTS details:
    • Each search tree edge $(s, a)$ stores prior probability $P(s, a)$, visit count $N(s, a)$, action value $Q(s, a)$.
    • Simulation begins from the root state, iteratively selects moves that maximise upper confidence bound $Q(s, a) + U(s, a)$ where $U(s, a) \propto P(s, a) / (1 + N(s, a))$ until leaf node encountered.
    • Leaf node expanded and evaluated only once by net to generate both the prior probabilities and evaluation $(P(s’, .), V(s’)) = f_\theta(s’)$.
    • Updates
    \[N(s, a) \leftarrow N(s, a) + 1 \\ Q(s, a) = 1/N(s, a) \sum_{s' \vert s, a \rightarrow s'} V(s')\]
    • $s, a \rightarrow s’$ means simulation eventually reached $s’$ after it took move $a$ from position $s$.

Page 4

Figure 1: Self-play reinforcement learning in AlphaGo Zero

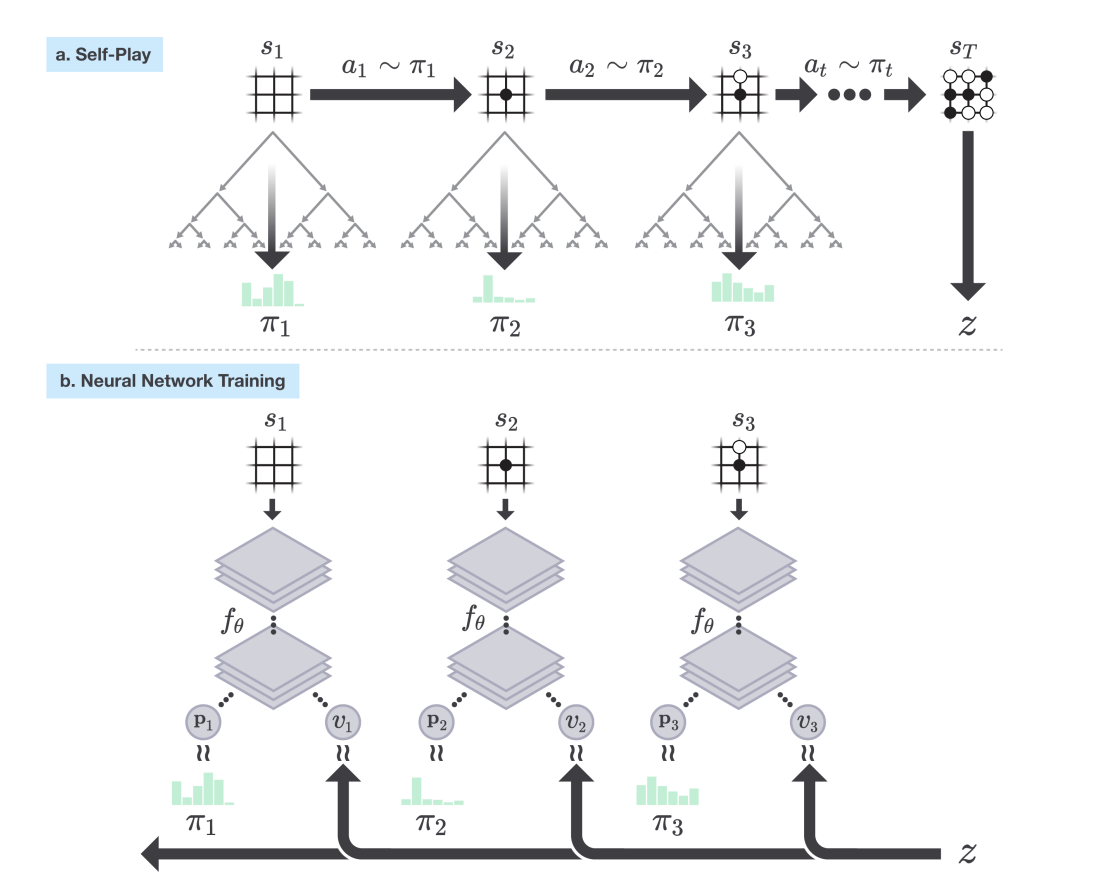
Figure 1 from the paper

Part (a)

  • Program plays a game $s_1 \ldots s_T$ against itself
  • In each position $s_t$ model executes MCTS using the latest version of the model $f_\theta$
  • Moves selected according to search probabilities computed by MCTS, $a_t \sim \pi_t$.
  • Terminal position $s_T$ scored according to game rules to compute winner $z$.

Part (b)

  • NN takes as input $s_t$, the raw board position and outputs a vector $\mathbf{p}_t$ representing probability distribution over moves and $v_t$ a scalar representing the probability of the current player winning in $s_t$
  • NN parameters $\theta$ updated to maximise similarity of the policy vector $\mathbf{p}_t$ to search probabilities $\boldsymbol{\pi}_t$
  • Also to minimise error between predicted winner $v_t$ and game winner $z$.
  • New parameters used in next iteration of self-play $\mathbf{a}$.

Page 5

  • Can view MCTS as a self-play algorithm that given $\theta$ and a root position $s$ computes a vector of search probabilities that recommend moves $\boldsymbol{\pi} = \alpha_\theta(s)$. where $\pi_a \propto N(s, a)^{1/\tau}$ - $\tau$-th root of visit count for each move for some temperature $\tau$.

  • NN trained by self-play RL algorithm that uses MCTS to play each move:
  • Init to random $\theta_0$
  • At each iteration $i$ games of self-play generated
  • At each time step $t$ MCTS search $\boldsymbol{\pi}_t$ is executed using previous iteration of NN $f_{\theta_{i-1}}$ and move is sampled from $\boldsymbol{\pi}_t$.
  • Game terminates at step $T$ when:
    • Both players pass; or
    • Search value <= resignation threshold; or
    • Exceeds max length
  • Game then score to give final reward $r_T=\pm 1$
  • Data for each time step: $(s_t, \boldsymbol{\pi}_t, z_t)$ where sign of $z_t$ depends on whether current player is winner.
  • New parameters $\theta_i$ trained from data $(s, \boldsymbol{\pi}, z)$ sampled uniformly among all time-steps of the last iteration of self-play.
  • NN adjusted to min error between pred value $v$ and self-play winner $z$ (using MSE) and NN move probabilities $\mathbf{p}$ and search probabilities $\boldsymbol{\pi}$ (using CE loss).
  • Total loss is a regularisation term plus sum of the two losses
Figure 2: Monte-Carlo tree search in AlphaGo Zero

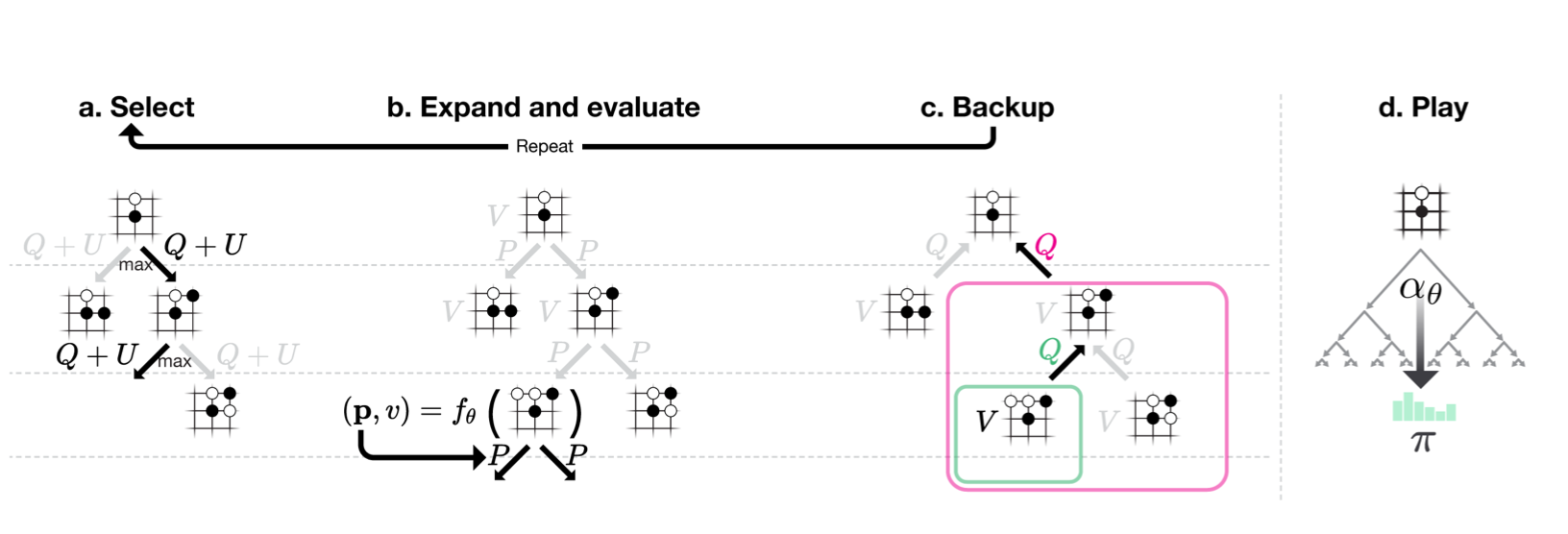
Figure 2 from the paper

  • Steps (a),(b),(c) repeated

Part (a) Select

  • Each simulation traverses tree by selected edge with max $Q + U$ (action-value + upper confidence bound)
  • $U$ depends on stored prior prob $P$ and visit count $N$ for edge which is incremented each time after it is traversed

Part (b) Expand and evaluate

  • Leaf node is expanded and NN is used to evaluate $P(s,\cdot) , V(s)$ for the associated position $s$
  • Outgoing edges from $s$ store $P$ which is a vector.

Part (c) Backup

  • Action values $Q$ updated to track mean of all evaluations $V$ in subtree below that action

Part (d) Play

  • Search probs $\boldsymbol{\pi}$ are returned proportional $N^{1/\tau}$:
    • $N$: visit count of each move from root state
    • $\tau$: parameter controlling temperature

2. Empirical Analysis of AlphaGo Zero Training

Page 6

  • 3 days of training involving 4.9 million self-play games, using 1600 simulations for each MCTS ~ 0.4s thinking time per move.
  • 700k mini-batches of 2048 positions used to update $\theta$

Page 7

Figure 3: Empirical evaluation of AlphaGo Zero

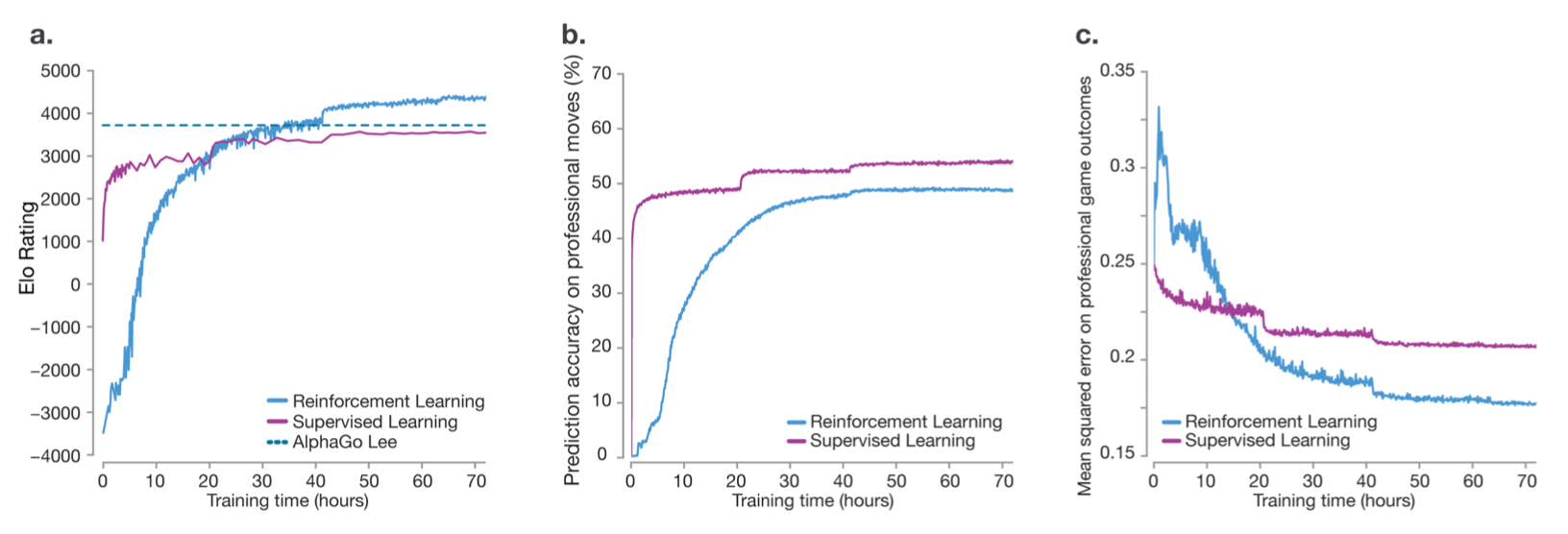
Figure 3 from the paper

Part (a)

  • RL versus supervised learning from human data. Smooth progression of learning - no oscillations or catastrophic forgetting
  • AlphaGo Zero outperformed AlphaGo Lee after just 36 hours - latter trained over several months
  • Using a single machine with 4 TPUs fully trained model defeated AlphaGo Lee by 100 games to 0.

Part (b), (c)

  • Supervised learning better at predicting human professional moves and has better performance initially but after about 24 hours, RL takes over

Page 9

Figure 4: Comparison of neural network architectures in AlphaGo Zero and AlphaGo Lee

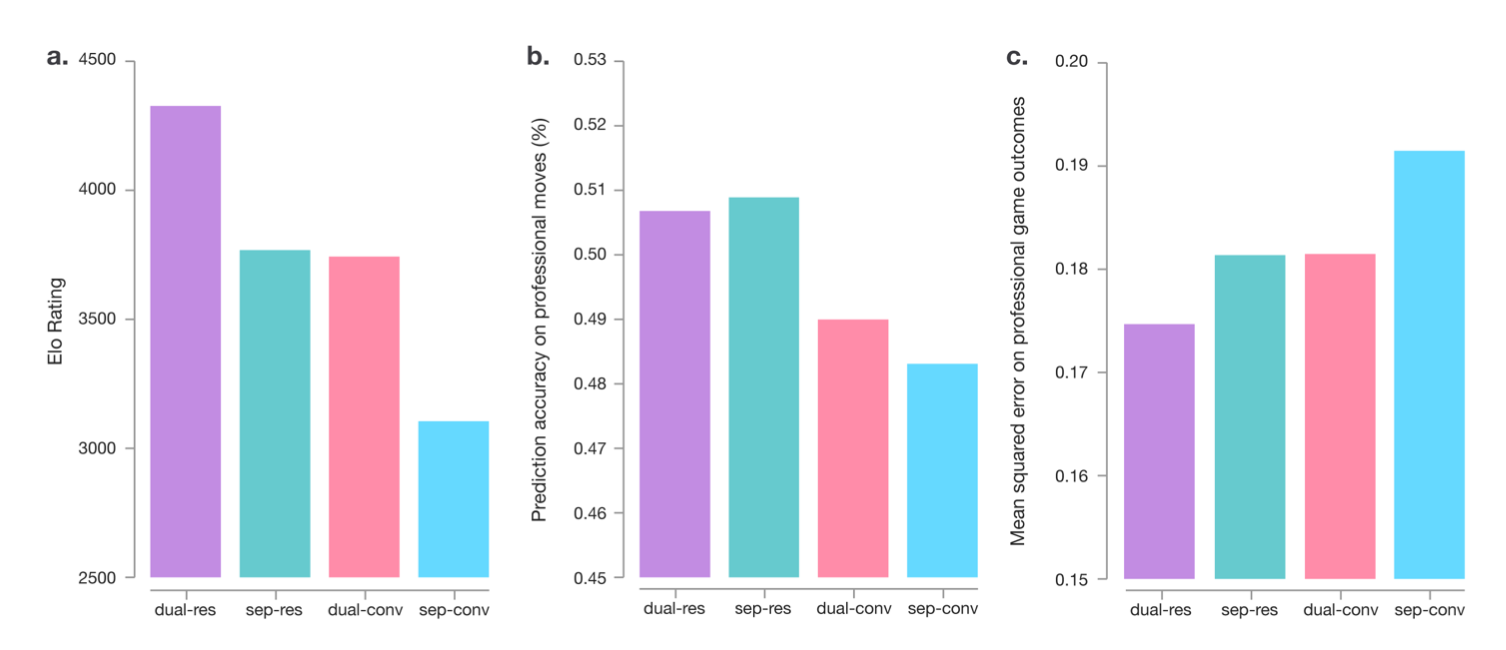
Figure 4 from the paper

  • Four different models that used either separate or combined policy and value networks (“dual”) and residual or convolutional architectures
  • Each net trained to min same loss function using a fixed dataset of self-play games generated by AlphaGo Zero after 72 hours of self-play training.

Part (a)

  • Each model was combined with AlphaGo Zero’s search to obtain a different player
  • Elo ratings were computed from eval games between the different players - 5s thinking time per move

Part (b), (c)

  • Residual nets more accurate at predicting human moves and had lower error at predicting professional game outcomes.

3. Knowledge Learned by AlphaGo Zero

Page 10

  • AlphaGo Zero managed to discover existing corner sequences (joseki) but ultimately preferred ones that were previously unknown
  • From entirely random moves, AlphaGo Zero rapidly went towards a sophisticated understanding of Go concepts
  • But one of the first elements learned by humans (schicho) was only understood by AlphaGo Zero much later in training

4. Final Performance of AlphaGo Zero

Page 10

  • Larger NN and longer duration
  • Trained from scratch for ~40 days
  • 29 million games of self-play were generated and the weights were updated from 3.1 million mini-batches of 2,048 positions each.
  • NN had 40 res blocks

Page 12

  • Overtook AlphaGo Lee by a lot after a few days but took over a month to overtakeAlphaGo Master by only a little (Figure 6a)
  • Evaluated using internal tournament against the following models, all of which it outperformed:
    • AlphaGo Fan (defeated Fan Hui)
    • AlphaGo Lee (defeated Lee Sedol)
    • AlphaGo Master (based on same algorithm and architecture but using human data and features, which defeated top human professionals 60-0 in online games)
    • Raw version of AlphaGo Zero which selects move $a$ with max probability $p_a$ without MCTS
    • Previous algorithms for GO
  • AlphaGo Zero won 89 games to 11 when evaluated head to head against AlphaGo Master in a 100 game match with 2 hour time controls

5. Conclusion

Paper results have demonstrated:

  • Pure RL approach is fully feasible even in the most challenging of domains
  • Possible to train to superhuman level without human supervision beyond basic rules about domain
  • Trains faster and gets much better asymptotic performance compared to training on expert data