In this post I share some notes about the Stirling cycle with derivations of quantities for each process along with code to plot P-V and S-T diagrams for a numerical example.

Contents

Preliminaries

from IPython.display import display
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pickle
import io


# A function to copy a matplotlib figure (adapted from https://stackoverflow.com/questions/45810557/copy-an-axes-content-and-show-it-in-a-new-figure)
def copy_fig(fig):
    buf = io.BytesIO()
    pickle.dump(fig, buf)
    buf.seek(0)
    return pickle.load(buf)

Equations overview

From experimental observations of ideal gases we have the following:

  1. P-V-T relation: $PV = mRT$ (equation of state)
  2. If $V$ is constant during a heat transfer $Q$, the gas behaves like a solid: $Q_{12} = mc_V(T_2 - T_1)$
  3. If the gas is subject to a constant temperature expansion / compression, we observe that $Q_{12} = W_{12}$

From which the following constitutive relations may be derived for energy and entropy

  • Constant volume heat transfer:
\[\Delta E = Q_{12} = mc_V(T_2 - T_1)\]
  • Entropy change for a reversible process:

\(\Delta S = mc_V\ln\frac{T_2}{T_1} + mR\ln{\frac{V_2}{V_1}}\)

  • P-V relation for isentropic process:
\[PV^{\gamma} = \text{constant} \\ \gamma = \frac{c_P}{c_V} = 1 + \frac{R}{c_V}\]

Efficiency (where $Q_C$ and $Q_H$ stand for the heat transferred out of and into the system, respectively). \(\eta = \frac{W_\text{net}}{Q_H}\)

Stirling cycle

  • Consists of four reversible processes
  • For each process we want to determine
    • Pressure volume (P-V) relation
    • Change in energy: $\Delta E$
    • Heat transfer: $Q$
    • Work: $W$
    • Change in entropy: $\Delta S$
    • The constituents of $\Delta S$:
      • Entropy transferred: $S_\text{trans}$
      • Entropy generated: $S_\text{gen}$
    • Entropy temperatue (S-T) relation
  • Since all the processes are reversible no entropy is generated so $S_\text{gen} = 0$

Process $1 \rightarrow 2$

  • Isothermal: $T_2 = T_1$
  • Expansion at $T_H = T_1$

Note that this is identical to process $1\rightarrow 2$ of the Carnot cycle

P-V relation

  • From equation of state
\[PV = mRT = mRT_1 \implies P = \frac{mRT_1}{V}\]

1st law

  • Since constant temperature expansion, from observation 3: \(\Delta E = 0\) \(Q_{12} = W_{12} = \int_1^2 P dV = \int_1^2 \frac{mRT}{V} dV = mRT_1\ln{\frac{V_2}{V_1}}\)

2nd law

  • Because of reversible and isothermal nature of the process, ${S_\text{gen}}$
\[\Delta S = \int_1^2 \frac{\delta Q}{T} + {S_\text{gen}}= \int_1^2\frac{\delta Q}{T} = \frac{1}{T_1}\int_1^2\delta Q = \frac{Q_{12}}{T_1} = mR\ln{\frac{V_2}{V_1}}\]
  • Since $S_\text{gen} = 0$
\[S_\text{trans} = \Delta S = mR\ln{\frac{V_2}{V_1}}\]

Summary

  • $P = \frac{mRT_1}{V}$
  • $\Delta E = 0$
  • $Q_{12} = mRT_1\ln{\frac{V_2}{V_1}}$
  • $W_{12} = mRT_1\ln{\frac{V_2}{V_1}}$
  • $\Delta S = mR\ln{\frac{V_2}{V_1}}$
    • $S_\text{trans} = mR\ln{\frac{V_2}{V_1}}$
    • $S_\text{gen} = 0$
  • On the $S-T$ diagram, since $T$ is constant, there is a straight horizontal line $T = T_1$ between $S_1$ and $S_2 = S_1 + mR\ln{\frac{V_2}{V_1}}$

Example

Some quanities for a cycle

cv = 718
R = 287
TH = 600
TC = 500
V1 = 0.01
V2 = 0.02
P1 = 1e6

We can derive other quantities from the above

T1 = TH
T2 = T1 # isothermal
# state equation to find P2 and m
m = P1 * V1 / (R * T1) 
P2 = m*R*T2/V2

print(f'm = {m}')
print(f'P2 = {P2}')

m = 0.05807200929152149
P2 = 500000.0

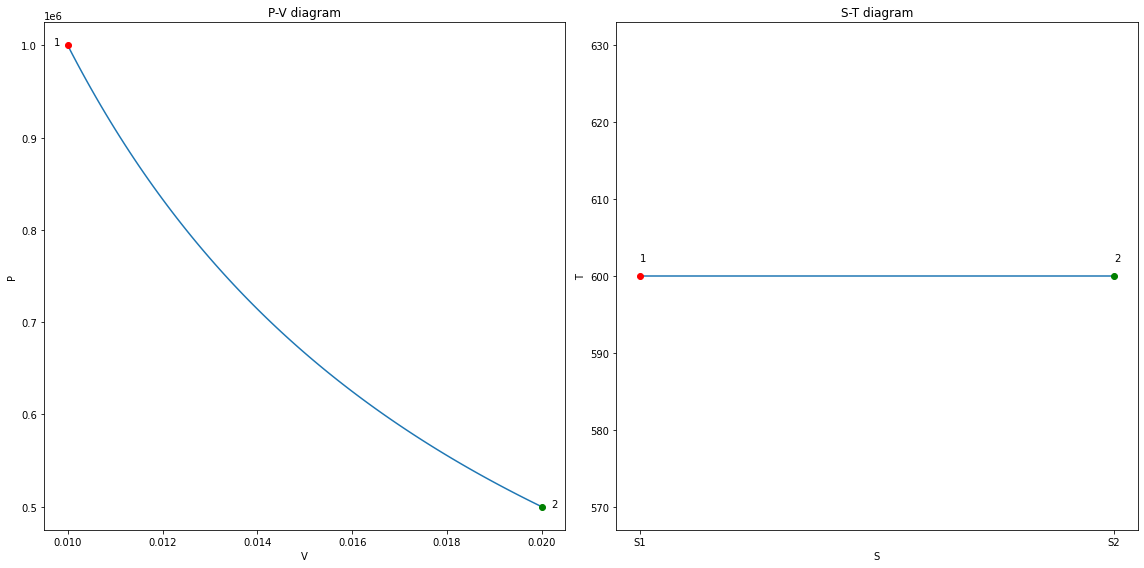
The P-V and S-T plots

V = np.linspace(V1, V2, 101)
P = m*R*T1 / V
assert np.isclose(P[-1], P2)
fig12, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 8))
ax1.plot(V, P)
line_clr = ax1.lines[0].get_color()
ax1.plot(V1, P1, marker='o', color='red')
ax1.plot(V2, P2, marker='o', color='green');
ax1.set_xlabel('V')
ax1.set_ylabel('P')
ax1.set_title('P-V diagram')
ax1.text(V1-3e-4, P1, '1')
ax1.text(V2 + 2e-4, P2, '2')


S1 = 1 # Some arbitrary value 
S2 = S1 + m*R*np.log(V2/V1)
ax2.plot(np.linspace(S1, S2, 101), np.ones(101)*T1)
ax2.plot(S1, T1, marker='o', color='red')
ax2.plot(S2, T2, marker='o', color='green');
ax2.text(S1, T1 + 2, '1')
ax2.text(S2, T2 + 2, '2')

ax2.set_xticks([S1, S2]);
ax2.set_xticklabels(['S1', 'S2']);
ax2.set_xlabel('S')
ax2.set_ylabel('T');
ax2.set_title('S-T diagram');

fig12.tight_layout();

png

state_df1 = pd.DataFrame(
    {'state': [1, 2],
     'P': [P1, P2],
     'V': [V1, V2],
     'T': [T1, T2]}
)

Q12 = m*R*T1*np.log(V2/V1)
W12 = Q12
dE = Q12 - W12
dS12 = S2 - S1
S_trans_12 = dS12
S_gen_12 = 0

process_df1 = pd.DataFrame(
    {'process': ['1 → 2'],
     'ΔE': [dE],
     'Q': [Q12],
     'W': [W12],
     'ΔS': [dS12],
     'S_trans': [S_trans_12],
     'S_gen': [S_gen_12]
    }
)

display(state_df1.round(5))
display(process_df1.round(5))
state P V T
0 1 1000000.0 0.01 600
1 2 500000.0 0.02 600
process ΔE Q W ΔS S_trans S_gen
0 1 → 2 0.0 6931.47181 6931.47181 11.55245 11.55245 0

Process $2 \rightarrow 3$

  • Ischoric (constant volume)
  • Cooling to $T_C = T_3 < T_2$

P-V relation

  • From equation of state, with $V_3 = V_2$
\[P_3 = mRT_3/V_3\]

1st Law

  • Isochoric so $W_{23} = 0$
\[\Delta E = Q_{23} = mc_V(T_3 - T_2)\]

2nd law

  • Since constant volume
\[S - S_1 = mc_V\ln\frac{T}{T_2} \implies \Delta S = mc_V\ln\frac{T_3}{T_2}\]

Summary

  • On the $P-V$ diagram, since $V$ is constant, there is a straight vertical with $P_3 = mRT_3/V_3$ and $P_2$ at each end
  • $\Delta E = mc_V(T_3 - T_2)$
  • $Q_{23} = mc_V(T_3 - T_2)$
  • $W_{23} = 0$
  • $\Delta S = mc_V\ln\frac{T_3}{T_2}$
    • $S_\text{trans} = mc_V\ln\frac{T_3}{T_2}$
    • $S_\text{gen} = 0$
  • $S = S_2 + mc_V\ln\frac{T}{T_2}$

Example (continued)

T3 = TC
gamma = 1 + R/cv
print(f'gamma = {gamma}')
V3 = V2
print(f'V3 = {V3}')
P3 = m * R * T3 / V3
print(f'P3 = {P3}')

gamma = 1.3997214484679665
V3 = 0.02
P3 = 416666.6666666667

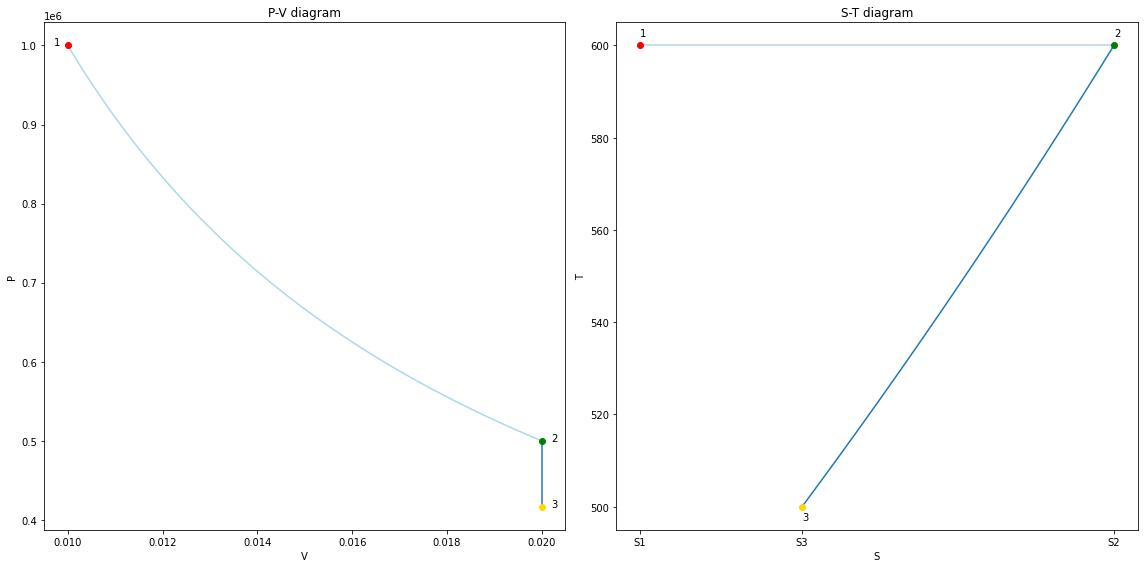
V = np.ones(101) * V2
P = np.linspace(P2, P3, 101)
assert np.isclose(P[-1], P3)
fig23 = copy_fig(fig12)
ax1, ax2 = fig23.get_axes()
for line in ax1.lines + ax2.lines:
    if line.get_color() == line_clr:
        line.set_color('lightblue')
ax1.plot(V, P, color=line_clr, zorder=-1)
ax1.plot(V3, P3, marker='o', color='gold');
ax1.text(V3 + 2e-4, P3, '3')
T = np.linspace(T2, T3, 101)
S = S2 + cv * m * np.log(T/T2) 
S3 = S2 + cv * m * np.log(T3/T2) 
assert np.isclose(S[-1], S3)
ax2.plot(S, T, color=line_clr, zorder=-1)
ax2.plot(S3, T3, marker='o', color='gold');

ax2.set_xticks([S1, S2, S3]);
ax2.set_xticklabels(['S1', 'S2', 'S3']);
ax2.text(S3, T3 - 3, '3')
fig23.tight_layout();
fig23

png

state_df2 = pd.concat(
    [state_df1, 
    pd.DataFrame(
        {'state': [3],
         'P': [P3],
         'V': [V3],
         'T': [T3]}
    )], axis=0
).reset_index(drop=True)

Q23 = m*cv*(T3 - T2) 
W23 = 0
dE = Q23 - W23
dS23 = S3 - S2
S_trans_23 = dS23
S_gen_23 = 0

process_df2 = pd.concat(
    [process_df1, 
     pd.DataFrame(
    {'process': ['2 → 3'],
     'ΔE': [dE],
     'Q': [Q23],
     'W': [W23],
     'ΔS': [dS23],
     'S_trans': [S_trans_23],
     'S_gen': [S_gen_23]
    })
    ], axis=0
)

display(state_df2.round(5))
display(process_df2.round(5))
state P V T
0 1 1000000.00000 0.01 600
1 2 500000.00000 0.02 600
2 3 416666.66667 0.02 500
process ΔE Q W ΔS S_trans S_gen
0 1 → 2 0.00000 6931.47181 6931.47181 11.55245 11.55245 0
0 2 → 3 -4169.57027 -4169.57027 0.00000 -7.60203 -7.60203 0

Process $3 \rightarrow 4$

  • Isothermal
  • Compression at $T_C = T_3$

The derivations are analogous to $1 \rightarrow 2$ so we can just need to replace the process ids in the results obtained earlier.

Note also that this is too is identical to process $3 \rightarrow 4$ of the Carnot cycle

Summary

  • $P = \frac{mRT_3}{V}$
  • $\Delta E = 0$
  • $Q_{34} = mRT_3\ln{\frac{V_4}{V_3}}$
  • $W_{34} = mRT_3\ln{\frac{V_4}{V_3}}$
  • $\Delta S = mR\ln{\frac{V_4}{V_3}}$
    • $S_\text{trans} = mR\ln{\frac{V_4}{V_3}}$
    • $S_\text{gen} = 0$
  • On the $S-T$ diagram, since $T$ is constant, there is a straight horizontal line $T = T_3$ between $S_3$ and $S_4=S_3 + mR\ln{\frac{V_4}{V_3}}$

Example (continued)

Note that to for $V_4$ we use the fact that the next process is isochoric

T4 = T3
V4 = V1
P4 = m*R*T4/V4

print(f'V4 = {V4}')
print(f'P4 = {P4}')

V4 = 0.01
P4 = 833333.3333333334

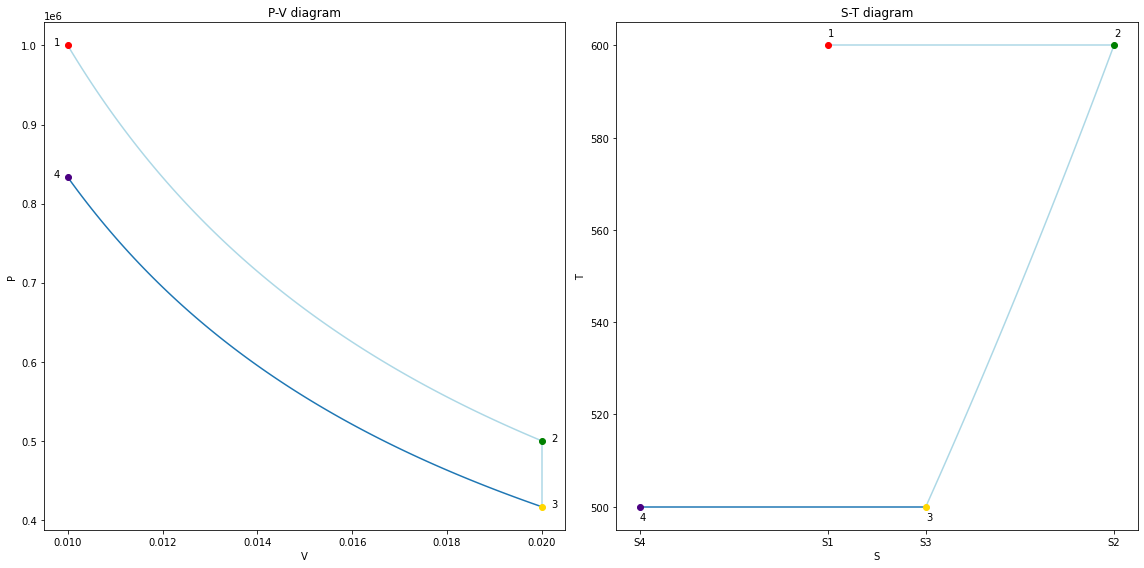
V = np.linspace(V3, V4, 101)
P = m*R*T3/V
assert np.isclose(P[-1], P4)
fig34 = copy_fig(fig23)
ax1, ax2 = fig34.get_axes()
for line in ax1.lines + ax2.lines:
    if line.get_color() == line_clr:
        line.set_color('lightblue')
ax1.plot(V, P, color=line_clr, zorder=-1)
ax1.plot(V4, P4, marker='o', color='indigo');
ax1.text(V4 - 3e-4, P4, '4')

S4 = S3 + m*R*np.log(V4/V3)
ax2.plot(np.linspace(S3, S4, 101), np.ones(101)*T3, color=line_clr, zorder=-1)
ax2.plot(S4, T4, marker='o', color='indigo');
ax2.text(S4, T4 - 3, '4')

ax2.set_xticks([S1, S2, S3, S4]);
ax2.set_xticklabels(['S1', 'S2', 'S3', 'S4']);
fig34.tight_layout();
fig34

png

state_df3 = pd.concat(
    [state_df2,
    pd.DataFrame(
        {'state': [4],
         'P': [P4],
         'V': [V4],
         'T': [T4]}
    )], axis=0
).reset_index(drop=True)

Q34 = m*R*T3*np.log(V4/V3)
W34 = Q34
dE = Q34 - W34
dS34 = S4 - S3
S_trans_34 = dS34
S_gen_34 = 0

process_df3 = pd.concat(
    [process_df2, 
     pd.DataFrame(
    {'process': ['3 → 4'],
     'ΔE': [dE],
     'Q': [Q34],
     'W': [W34],
     'ΔS': [dS34],
     'S_trans': [S_trans_34],
     'S_gen': [S_gen_34]
    })
    ], axis=0
)

display(state_df3.round(5))
display(process_df3.round(5))
state P V T
0 1 1000000.00000 0.01 600
1 2 500000.00000 0.02 600
2 3 416666.66667 0.02 500
3 4 833333.33333 0.01 500
process ΔE Q W ΔS S_trans S_gen
0 1 → 2 0.00000 6931.47181 6931.47181 11.55245 11.55245 0
0 2 → 3 -4169.57027 -4169.57027 0.00000 -7.60203 -7.60203 0
0 3 → 4 0.00000 -5776.22650 -5776.22650 -11.55245 -11.55245 0

Process $4 \rightarrow 1$

  • Isochoric
  • Heating to $T_H = T_1$

The derivations are analogous to $2 \rightarrow 3$ so we can just need to replace the process ids in the results obtained earlier

Summary

  • On the $P-V$ diagram, since $V$ is constant, there is a straight vertical with $P_1 = mRT_1/V_1$ and $P_4$ at each end
  • $\Delta E = mc_V(T_1 - T_4)$
  • $Q_{41} = mc_V(T_1 - T_4)$
  • $W_{41} = 0$
  • $\Delta S = mc_V\ln\frac{T_4}{T_1}$
    • $S_\text{trans} = mc_V\ln\frac{T_4}{T_1}$
    • $S_\text{gen} = 0$
  • $S = S_4 + mc_V\ln\frac{T}{T_4}$
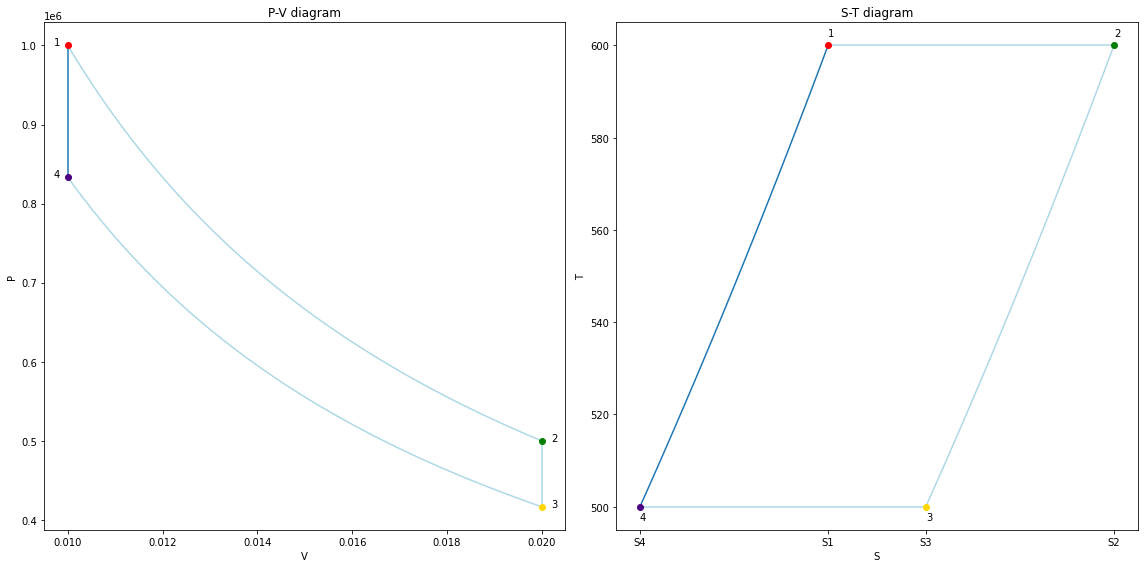
V = np.ones(101) * V4
P = np.linspace(P4, P1, 101)
assert np.isclose(P[-1], P1)
fig41 = copy_fig(fig34)
ax1, ax2 = fig41.get_axes()
for line in ax1.lines + ax2.lines:
    if line.get_color() == line_clr:
        line.set_color('lightblue')
ax1.plot(V, P, color=line_clr, zorder=-1)
T = np.linspace(T4, T1, 101)
S = S4 + cv * m * np.log(T/T4) 
assert np.isclose(S[-1], S1)
ax2.plot(S, T, color=line_clr, zorder=-1)

fig41

png

Q41 = m*cv*(T1 - T4) 
W41 = 0
dE = Q41 - W41
dS41 = S1 - S4
S_trans_41 = dS41
S_gen_41 = 0

process_df4 = pd.concat(
    [process_df3, 
     pd.DataFrame(
    {'process': ['4 → 1'],
     'ΔE': [dE],
     'Q': [Q41],
     'W': [W41],
     'ΔS': [dS41],
     'S_trans': [S_trans_41],
     'S_gen': [S_gen_41]
    })
    ], axis=0
)

display(state_df3.round(5))
display(process_df4.round(5))
state P V T
0 1 1000000.00000 0.01 600
1 2 500000.00000 0.02 600
2 3 416666.66667 0.02 500
3 4 833333.33333 0.01 500
process ΔE Q W ΔS S_trans S_gen
0 1 → 2 0.00000 6931.47181 6931.47181 11.55245 11.55245 0
0 2 → 3 -4169.57027 -4169.57027 0.00000 -7.60203 -7.60203 0
0 3 → 4 0.00000 -5776.22650 -5776.22650 -11.55245 -11.55245 0
0 4 → 1 4169.57027 4169.57027 0.00000 7.60203 7.60203 0

Efficiency

\[W_\text{net} = W_{12} + W_{23} + W_{34} + W_{41} \\ = mRT_1\ln{\frac{V_2}{V_1}} + 0 + mRT_3\ln{\frac{V_4}{V_3}} + 0\]

Since

\(V_3 = V_2\) \(V_4 = V_1\)

we have

\[\frac{V_3}{V_4} = \frac{V_2}{V_1}\]

Hence

\[W_\text{net} = mR(T_1 - T_3)\ln{\frac{V_2}{V_1}} = mR(T_H - T_C)\ln{\frac{V_2}{V_1}}\]

Note that we also need to include an additional term heat transfer term $Q_{41}$ which was absent in the Carnot cycle since process $4 \rightarrow 1$ of the Carnot cycle was adiabatic.

\[Q_H = Q_{41} + Q_{12} = mc_V(T_1 - T_4) + mRT_1\ln{\frac{V_2}{V_1}} = mc_V(T_H - T_C) + mRT_H\ln{\frac{V_2}{V_1}}\]

which means

\[\eta = \frac{W_\text{net}}{Q_H} = \frac{mR(T_H - T_C)\ln{\frac{V_2}{V_1}}}{mc_V(T_H - T_C) + mRT_H\ln{\frac{V_2}{V_1}}} \\= \frac{1}{\frac{c_V}{R}\frac{1}{\ln{\frac{V_2}{V_1}}} + \frac{T_H}{T_H - T_C} }\]

Note that since $V_2 > V_1 \implies \frac{c_V}{R}\ln{\frac{V_2}{V_1}} > 0$

\[\eta_\text{Stirling} = \frac{1}{\frac{c_V}{R}\frac{1}{\ln{\frac{V_2}{V_1}}} + \frac{1}{\eta_\text{Carnot}} } = \frac{\eta_\text{Carnot}}{\eta_\text{Carnot}\frac{c_V}{R}\frac{1}{\ln{\frac{V_2}{V_1}}} + 1 } < \eta_\text{Carnot}\]

This reduction in efficiency is due to the fact that heat transfer occurs with a change in temperature in contrast to the purely isothermal heat transfers found in the Carnot cycle.

Summary

fig_final = copy_fig(fig41)
ax1, ax2 = fig_final.get_axes()
for line in ax1.lines + ax2.lines:
    if line.get_color() == 'lightblue':
        line.set_color(line_clr)
display(fig_final)
display(state_df3.round(5))
display(process_df4.round(5))

png

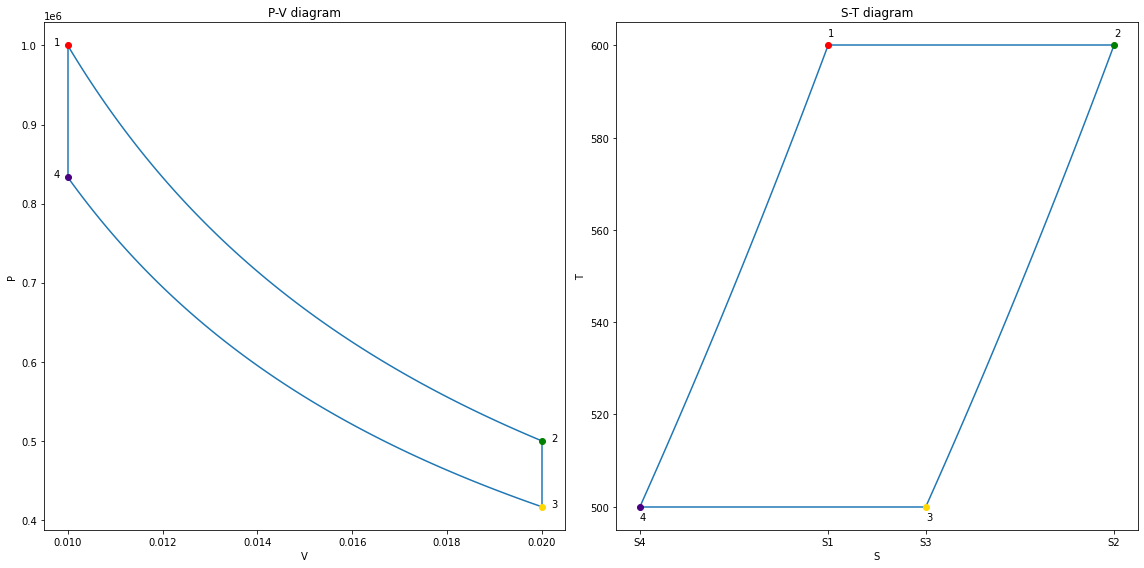
state P V T
0 1 1000000.00000 0.01 600
1 2 500000.00000 0.02 600
2 3 416666.66667 0.02 500
3 4 833333.33333 0.01 500
process ΔE Q W ΔS S_trans S_gen
0 1 → 2 0.00000 6931.47181 6931.47181 11.55245 11.55245 0
0 2 → 3 -4169.57027 -4169.57027 0.00000 -7.60203 -7.60203 0
0 3 → 4 0.00000 -5776.22650 -5776.22650 -11.55245 -11.55245 0
0 4 → 1 4169.57027 4169.57027 0.00000 7.60203 7.60203 0